- Standalone Applications
- BioEddie
- Chemaxon Assay
- ChemCurator
- Chemicalize
- ChemLocator
- cHemTS
- Compliance Checker
- Compound Registration
- Quick Start Guide
- Compound Registration User's Guide
- Overview
- Compound Registration Abbreviations
- Definitions of Terms
- Compound Registration Introduction
- Login
- Dashboard page
- Autoregistration
- Bulk Upload
- Advanced Registration
- Search
- User Profile
- Browse page
- Appendix A. Calculations
- Appendix B. Markush Structures
- Multi-Component compounds
- Restricted compounds
- Configuration Guide
- Deployment Guide
- Compound Registration FAQ
- Compound Registration System Requirements
- Compound Registration History of Changes
- API documentation
- Instant JChem
- Instant Jchem User Guide
- Getting Started
- IJC Projects
- IJC Schemas
- Viewing and Managing Data
- Lists and Queries
- Collaboration
- Import and Export
- Editing Databases
- Relational Data
- Chemical Calculations and Predictions
- Chemistry Functions
- Security
- Scripting
- Updating Instant JChem
- Tips and Tricks
- Instant JChem Tutorials
- Building a relational form from scratch
- Building more complex relational data models
- Defining a security policy
- Filtering items using roles
- Lists and Queries management
- Query building tutorial
- Reaction enumeration analysis and visualization
- SD file import basic visualization and overlap analysis
- Using Import map and merge
- Using Standardizer to your advantage
- Pivoting tutorial
- Instant JChem Administrator Guide
- Admin Tool
- IJC Deployment Guide
- Supported databases
- JChem Cartridge
- Using Oracle Text in Instant JChem
- JChem Postgres Cartridge in IJC
- Deployment via Java Web Start
- Startup Options
- Shared project configuration
- Accessing data with URLs
- Instant JChem Meta Data Tables
- Test to Production Metadata Migrator
- Filtering Items
- Deploying the IJC OData extension into Spotfire
- Reporting a Problem
- Manual Instant JChem schema admin functions
- SQL Scripts for Manual Schema Upgrade
- Database Row Level Security
- JccWithIJC
- Instant JChem Developer Guide
- Working With IJC Architecture
- IJC API
- Groovy Scripting
- Good Practices
- Schema and DataTree Scripts
- Simple SDF Exporter
- Relational SDF Exporter
- CDX File Importer
- Data Merger or Inserter from an SDF file
- Markush DCR Structures Exporter
- Select Representative Member of Clusters
- Table Standardizer
- Populate a Table with Microspecies
- Create a Diverse Subset
- Pearson Linear Correlation Co-efficient Calculator
- PDF Trawler
- Simple Substructure Search
- Intersecting Sets
- Find Entries with Duplicated Field Value
- Importing Multiple SDF Files
- Calling External Tools
- Create Relational Data Tree
- Forms Model Scripts
- Button Scripts
- Execute Permanent Query
- Patent Fetcher Button
- Batch Searching Button
- Import or Export a Saved Query SDF Button
- Back and Next Buttons
- Add Annotations Button
- Simple Structure Checker Button
- Advanced Structure Checker Button
- Calculate MolWeight and generate SMILES
- Get Current User
- Simple ChemicalTerms evaluator
- Edit Molecule Button
- TanimotoMultiple
- Execute Permanent Query Based On Its Name
- Open existing view in the same dataTree
- Export selection to file
- Generate random resultset from actual resultset
- Form Scripts
- Groovy Scriptlets
- Buttons vs Scripts
- Creating New Entities
- Creating New Fields
- Reading Molecules From a File
- Insert or Update a Row
- Evaluator
- Create or Find a Relationship
- Adding an Edge to a Data Tree
- Exporting Data to a File
- Connect to an External Database
- Create a New ChemTerm Field
- Create a New Dynamic URL Field
- Create a New Static URL Field
- Java Plugins
- IJC Plugin Quick Start
- IJC Hello World Plugin
- IJC Plugin tutorial - MyAddField plugin
- IJC Plugin tutorial - MyMathCalc plugin
- IJC Plugin tutorial - Renderer Example
- IJC Plugin tutorial - MySCServer webapp
- IJC Plugin tutorial - MySCClient plugin
- IJC Plugin tutorial - Canvas widget
- Java Plugins and Java Web Start
- Instant JChem FAQ
- Instant JChem Installation and Upgrade
- Instant JChem Licensing
- IJC Getting Help and Support
- Instant JChem System Requirements
- Instant JChem History of Changes
- Instant Jchem User Guide
- Markush Editor
- Design Hub
- History of changes
- Install guide
- Configuration guide
- Plugin Catalogue
- Developer guide - REST API
- Developer guide - resolver plugins
- Developer guide - real time plugins
- Developer guide - real time plugin templates
- Developer guide - export plugins
- Developer guide - storage plugins
- Developer guide - company support plugins
- Developer guide - import plugins
- Developer guide - registry plugins
- Developer guide - theme customization
- Install guide - Kubernetes
- Marvin Desktop Suite
- MarvinSketch
- User Guide
- Getting Started
- Graphical User Interface
- Working in MarvinSketch
- Structure Display Options
- Basic Editing
- Drawing Simple Structures
- Drawing More Complex Structures
- Drawing Reactions
- Using Integrated Calculations
- Graphical Objects
- Import and Export Options
- Multipage Documents
- Printing
- Chemical Features
- Marvin OLE User Guide
- Appendix
- Tutorials
- Developer Guide
- MarvinSketch Application Options
- User Guide
- MarvinView
- Marvin Bundles
- Marvin Desktop Suite Installation and Upgrade
- Marvin Desktop Suite History of Changes
- Marvin Desktop Suite Licensing
- MarvinSketch
- Molconvert
- Plexus Connect
- Plexus Connect - Quick Start Guide
- Plexus Connect - User Guide
- Plexus Connect - Log in
- Plexus Connect - Dashboard
- Plexus Connect - Exporting Your Data
- Plexus Connect - Export Templates
- Plexus Connect - Browsing in Your Data Set
- Plexus Connect - Selecting Data
- Plexus Connect - Searching in Your Database
- Plexus Connect - Saved Queries
- Plexus Connect - List Management
- Plexus Connect - Sorting Data
- Plexus Connect - Sharing Data with Other Users
- Plexus Connect - Charts View
- Plexus Connect - R-group Decomposition
- Plexus Connect - Administrator Guide
- Plexus Connect - Authentication
- Plexus Connect - Sharing Schema Items Among Users
- Plexus Connect - Business Flags
- Plexus Connect - Row-level Security
- Plexus Connect - Shared data sources
- Plexus Connect - Plexus storage
- Plexus Connect - Configuration Files
- Plexus Connect - Simple table
- Plexus Connect - Getting the Plexus Backend and Frontend Log Files
- Plexus Connect - Form Editor
- Plexus Connect - Scripting
- Plexus Connect - API keys
- Plexus Connect - Deploying Spotfire Middle Tier solution
- Plexus Connect - Installation and System Requirements
- Plexus Connect - Licensing
- Plexus Connect - Getting Help and Support
- Plexus Connect - FAQ
- Plexus Connect - Privacy Policy
- Plexus Connect - Terms of Use for the Demo Site
- Plexus Connect - History of Changes
- Plexus Connect - Schema Refresh Without Restart
- Trainer Engine
- Toolkits and Components
- AutoMapper
- Calculator Plugins
- Introduction to Calculator Plugins
- Calculator Plugins User's Guide
- Calculator Plugins Developer's Guide
- Calculators on AWS Marketplace
- Calculators in Playground
- Background materials
- Calculation of partial charge distribution
- Generate3D
- Isoelectric point (pI) calculation
- LogP and logD calculations
- NMR model prediction
- pKa calculation
- Red and blue representation of pKa values
- Tautomerization and tautomers
- Validation results
- Tautomerization and tautomer models of Chemaxon
- Theory of aqueous solubility prediction
- The tautomerization models behind the JChem tautomer search
- Calculators performance reports
- Calculator Plugins Licensing
- Calculator Plugins FAQ
- Calculator Plugins Getting Help and Support
- Calculator Plugins History of Changes
- Calculator Plugins System Requirements
- Biomolecule Toolkit
- Chemaxon .NET API
- Chemaxon Synergy
- Chemaxon Synergy User Guide
- Chemaxon Synergy Developer Guide
- Chemaxon Synergy Administrator Guide
- Chemaxon Synergy History of Changes
- Chemaxon Cloud
- Document to Structure
- JChem Base
- JChem Base Administration
- JChem Base Developer's Guide
- JChem Base User's Guide
- Query Guide
- Search types
- Similarity search
- Query features JCB
- Stereochemistry JCB
- Special search types
- Search options
- Atomproperty specific search options
- Attached data specific search options
- Bond specific search options
- Chemical terms specific search options
- Database specific search options
- General search options
- Hitdisplay specific search options
- Markush structure specific search options
- Performance specific search options
- Polymer specific search options
- Query feature specific search options
- Reaction specific search options
- Resultset specific search options
- Similarity specific search options
- Stereo specific search options
- Tautomer specific search options
- Tautomer search - Vague bond search - sp-Hybridization
- Standardization JCB
- Hit display-coloring
- Appendix JCB
- Matching Query - Target Examples
- jcsearch Command Line Tool
- jcunique Command Line Tool
- Homology Groups in Markush Structures
- Query Guide
- JChem Base FAQ
- JChem Base History of Changes
- JChem Base Getting Help and Support
- JChem Choral
- JChem Oracle Cartridge
- JChem Microservices
- JChem PostgreSQL Cartridge
- Getting Started JChem PostgreSQL Cartridge
- JChem PostgreSQL Cartridge Manual
- Second Generation Search Engine
- JChem PostgreSQL Cartridge FAQ and Known Issues
- JChem PostgreSQL Cartridge History of Changes
- JChem PostgreSQL Cartridge Getting Help and Support
- JChem PostgreSQL Cartridge Licensing
- Comparison of JChem PostgreSQL Cartridge and JChem Oracle Cartridge
- Migration Guide
- JKlustor
- Markush Tools
- Marvin JS
- User Guide
- Getting Started
- Editor Overview
- Editor Canvas
- Dialogs
- Toolbars
- Context Menus
- Drawing and Editing Options
- Feature Overview Pages
- Keyboard Shortcuts
- Developer Resources
- History of Changes
- Frequently Asked Questions
- Video Tutorials
- Comparison of Marvin JS and MarvinSketch Feature Sets
- User Guide
- Marvin Pro
- Name to Structure
- Reactor
- Reactor User's Guide
- Introduction to Reactor
- Reactor Getting Started
- Reactor Concepts
- Reactor Examples
- Working with Reactor
- Specifying Reactions
- Specifying Reactants
- Reaction Mapping
- Reaction Rules
- Reactant Combinations
- Running Reactor
- Reactor Interfaces
- Reactor Application
- Reactor Command-line Application
- Reactor in Instant JChem
- Reactor in JChem for Excel
- Reactor in KNIME
- Reactor in Pipeline Pilot
- Reactor in Plexus Suite
- API, Web Services
- Glossary
- Reactor FAQ
- Reactor Licensing
- Reactor Getting Help and Support
- Reactor History of Changes
- Reactor Configuration Files
- Reactor User's Guide
- Screen
- Standardizer
- Standardizer User's Guide
- Standardizer Introduction
- Standardizer Getting Started
- Standardizer Concepts
- Working with Standardizer
- Standardizer Actions
- Add Explicit Hydrogens
- Alias to Atom
- Alias to Group
- Aromatize
- Clean 2D
- Clean 3D
- Clear Isotopes
- Clear Stereo
- Contract S-groups
- Convert Double Bonds
- Convert Pi-metal Bonds
- Convert to Enhanced Stereo
- Create Group
- Dearomatize
- Disconnect Metal Atoms
- Expand S-groups
- Expand Stoichiometry
- Map
- Map Reaction
- Mesomerize
- Neutralize
- Remove Absolute Stereo
- Remove Atom Values
- Remove Attached Data
- Remove Explicit Hydrogens
- Remove Fragment
- Remove R-group Definitions
- Remove Stereo Care Box
- Replace Atoms
- Set Absolute Stereo
- Set Hydrogen Isotope Symbol
- Strip Salts
- Tautomerize
- Transform
- Ungroup S-groups
- Unmap
- Wedge Clean
- Remove
- Standardizer Transform
- Custom Standardizer Actions
- Remove Solvents
- Creating a Configuration Standardizer
- Interfaces Standardizer
- Standardizer File Formats
- Standardizer Actions
- Standardizer Developer's Guide
- Standardizer Installation and System Requirements
- Standardizer Licensing
- Standardizer Getting Help and Support
- Standardizer History of Changes
- Standardizer User's Guide
- Structure Checker
- Structure Checker User's Guide
- Introduction
- Structure Checker Getting Started
- Structure Checker Concepts
- Working with Structure Checker
- Checker List
- Abbreviated Group
- Absent Chiral Flag
- Absolute Stereo Configuration
- Alias
- Aromaticity Error
- Atom Map
- Atom Query Property
- Atom Value
- Atropisomer
- Attached Data
- Bond Angle
- Bond Length
- Bond Topology
- Brackets
- Chiral Flag
- Chiral Flag Error
- Circular R-group Reference
- Coordination System Error
- Covalent Counterion
- Crossed Double Bond
- Custom Checkers and Fixers
- Double Bond Stereo Error
- EZ Double Bond
- Empty Structure
- Explicit Hydrogen
- Explicit Lone Pairs
- Incorrect Tetrahedral Stereo
- Isotope
- Metallocene Error
- Missing Atom Map
- Missing R-group Reference
- Molecule Charge
- Multicenter
- Multicomponent
- Multiple Stereocenter
- Non-standard Wedge Scheme
- Non-stereo Wedge Bond
- OCR Error
- Overlapping Atoms
- Overlapping Bonds
- Pseudo Atom
- Query Atom
- Query Bond
- Racemate
- Radical
- Rare Element
- R-atom
- Reacting Center Bond Mark
- Reaction Map Error
- Relative Stereo
- R-group Attachment Error
- R-group Bridge Error
- R-group Reference Error
- Ring Strain Error
- Solvent
- Star Atom
- Stereo Care Box
- Stereo Inversion Retention Mark
- Straight Double Bond
- Substructure
- Three Dimension 3D
- Unbalanced Reaction
- Unused R-group Reference
- Valence Error
- Valence Property
- Wedge Error
- Wiggly Bond
- Wiggly Double Bond
- Creating a Configuration Structure Checker
- Interfaces of Structure Checker
- Checker List
- Structure Checker Developer's Guide
- Structure Checker Installation and System Requirements
- Structure Checker Licensing
- Structure Checker Getting Help and Support
- Structure Checker History of Changes
- Structure Checker User's Guide
- Structure to Name
- Third-party Integration
- JChem for Office
- Before Using
- Supported Versions
- Installation
- Administration
- Diagnostic Tool
- JChem for Excel User's Guide
- JChem for Excel Ribbon
- Working with Structures in Excel
- Add a Structure to a Cell
- Edit a Structure in a Cell
- Edit Structures in the Task Pane
- Resize Structures
- Structures in Merged Cells
- Show and Hide Structures
- Show and Hide Structures and Structure IDs
- Insert Single Structures
- Open Structure Files
- Delete Structures from a Selected Range
- Save Single Structure to a File
- Print Structures
- Copy and Paste with JChem for Excel
- Convert from Structures
- Convert to Structures
- Convert ISIS, ChemDraw, Accord, and Insight for Excel Files to JChem for Excel Files
- Calculations with Third-Party Services
- Specify External Image and Name Services
- Importing from Databases in JChem for Excel
- Manage Connections
- Add an Oracle Connection in JChem for Excel
- Add a MySQL Connection in JChem for Excel
- Add an MSSQL Connection in JChem for Excel
- Add a PostgreSQL Connection in JChem for Excel
- Add a JChem Web Services Connection in JChem for Excel
- Favorite Entities in JChem for Excel
- Edit and Delete Connections in JChem for Excel
- Import from Database in JChem for Excel
- Import from IJC Database in JChem for Excel
- Import from Database by IDs
- Manage Connections
- Resolve ID
- Import from File
- Export to File
- Share Excel Files
- R-group Decomposition in JChem for Excel
- SAR Table Generation
- Structure Filter
- Options in JChem for Excel
- General Options in JChem for Excel
- Database Connection Options
- Formatting Options
- Licensing Options in JChem for Excel
- File Import Options in JChem for Excel
- IJC Import Options in JChem for Excel
- File Export Options in JChem for Excel
- Printing Options in JChem for Excel
- Structure Sheet Options
- Image Conversion Options
- Structure Display Options in JChem for Excel
- Structure Editor Options in JChem for Excel
- Event Handling Options in JChem for Excel
- Actions
- Functions in JChem for Excel
- Custom Chemical Functions in JChem for Excel
- Use Custom Chemical Functions
- Functions Reference
- Normal
- Charge in JChem for Excel
- Chemical Terms in JChem for Excel
- Dissimilarity
- Drug Discovery Filtering in JChem for Excel
- Elemental Analysis in JChem for Excel
- Geometry in JChem for Excel
- Hydrogen Bond Donor-Acceptor in JChem for Excel
- Isomers in JChem for Excel
- Naming
- Protonation and Partitioning in JChem for Excel
- Solubility
- Tautomers in JChem for Excel
- Topology Analysis in JChem for Excel
- Structure in JChem for Excel
- Image
- Normal
- User Interface Customization in JChem for Excel
- Checking DirectX Information
- JChem for Office User's Guide
- JChem Ribbon
- Working with Structures
- Importing from Databases in JChem for Office
- Manage Connections in JChem for Office
- Add an Oracle Connection in JChem for Office
- Add a MySQL Connection in JChem for Office
- Add an MSSQL Connection in JChem for Office
- Add a PostgreSQL Connection in JChem for Office
- Add a JChem Web Services Connection in JChem for Office
- Favorite Entities in JChem for Office
- Edit and Delete Connections in JChem for Office
- Import from Database in JChem for Office
- Import from IJC Database
- Manage Connections in JChem for Office
- Import from File in Jchem for Office
- Options in JChem for Office
- Properties in JChem for Office
- Switching JChem for Office to Lite Mode
- JChem for Office Lite User's Guide
- JChem for Office Known Issues
- JChem for Office History of Changes
- Troubleshooting - JChem for Office
- KNIME Nodes
- Pipeline Pilot Components
- JChem for Office
- Cross-Product Documentation
- Chemaxon Configuration Folder
- Chemical Fingerprints
- Chemical Terms
- File Formats
- Basic export options
- Compression and Encoding
- Document formats
- Graphics Formats
- Molecule file conversion with Molconverter
- Molecule Formats
- CML
- MDL MOL files
- Daylight SMILES related formats
- Chemaxon SMILES extensions
- IUPAC InChI, InChIKey, RInChI and RInChIKey
- Name
- Sequences - peptide, DNA, RNA
- FASTA file format
- Protein Data Bank (PDB) file format
- Tripos SYBYL MOL and MOL2 formats
- XYZ format
- Gaussian related file formats
- Markush DARC format - VMN
- CSV
- Input and Output System
- License Management
- Long Term Supported Releases - LTS
- Notice about CAS Registry Numbers®
- Public Repository
- Scientific Background
- Structure Representation
- Structure Representation - Class Representation
- Aromaticity
- Implicit, Explicit and Query Hydrogens
- Assigning stereochemistry descriptors
- Cleaning options
- Deprecated and Removed Methods
- Relative configuration of tetrahedral stereo centers
- Iterator Factory
- Atom and bond-set handling
- Graphic object handling
- Supported Java Versions
- Legal
- Discontinued Products
- Document to Database
- Fragmenter
- JChem Neo4j Cartridge
- Markush Overlap
- MarvinSpace
- MarvinSpace User's Guide
- MarvinSpace Developer's Guide
- MarvinSpace History of Changes
- Metabolizer
- Plexus Suite
- Quick Start Guide - Plexus Suite
- Plexus Suite User Guide
- Log in to Plexus Suite
- The Plexus Suite Dashboard
- Importing New Data
- Exporting Your Data
- Browsing in Your Data Set
- Selecting Data
- Searching in Your Database
- Saved Queries
- List Management
- Sorting Data
- Sharing Data with Other Users
- Calculating Molecular Properties for Single Compounds
- Adding calculated columns to tables
- Scaffold Based Enumeration
- Reaction Based Enumeration
- Registering Molecules in the Corporate Database
- Charts view
- Plexus Suite Video Tutorials
- Plexus Suite Administrator Guide
- Plexus Suite Authentication
- Sharing Schema Items Among Users
- Business Flags
- Row-level Security
- Building blocks
- Admin Tools
- Adding JavaScript Files for Custom Functionality
- Writing JavaScript Files for Custom Functionality
- Integration with Chemaxon's Compound Registration System
- Shared data sources in Plexus Connect
- Configuration Files
- Edit Views
- Simple table
- Installation and System Requirements of Plexus Suite
- Plexus Suite Licensing
- Getting Help and Support for Plexus Suite
- Plexus Suite FAQ
- Plexus Suite Privacy Policy
- Terms of Use for the Plexus Suite Demo Site
- Plexus Suite History of Changes
- Schema Refresh Without Restart
- JChem Web Services Classic
pKa calculation
This background material explains the theory behind the pKa calculation:
Introduction
Chemical properties of molecules depend largely on whether they are ionized or not. Most organic molecules are capable of gaining and/or losing a proton in aqueous solutions. Proton transfer most frequently occurs between water and any ionizable atom of the organic molecule.
The molecule's response to protonation or de-protonation depends significantly on the site that was affected by the proton transfer. Partial charge distribution of the molecule also varies based on the protonation of the acid/base active sites. Since the partial charge distribution is very sensitive to the protonation/de-protonation process (both near and far from the affected site), it can be used to determine the p K a of a molecule.
Our p K a prediction program is based on the calculation of partial charge distribution of atoms in the molecule.
The concept of ionisation
Acidic and basic molecules are ionised in aqueous solution. Acidic or basic character is assigned to the molecule according to Brönsted's rule. The ratio of the ionised and neutral forms depends on the pH, the temperature and the ion activity of the bulk phase. The ionisation constant Ka is obtained from the activity ratio of conjugated base and conjugated acid multiplied with proton activity:
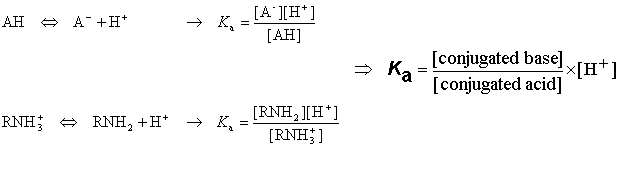
Definition of pKa
The p K a value is obtained from the ionisation constant of a molecule using the following definition:
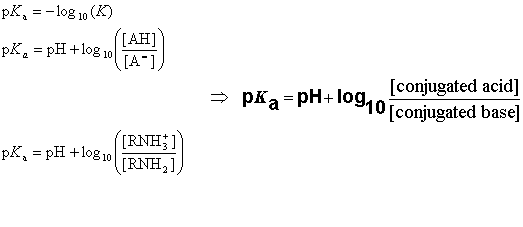
When the pH of the solution is equal with p K a, the concentrations of the dissociated and undissociated species are equal.
Definition of the acidic/basic prefix of pKa
Definition of the basic prefix
Protonated positive ions are considered as protonated basic sites , therefore "basic" prefix is used for them. The neutral basic sites are predefined in the p K a calculator, they also have the "basic" prefix, e.g. if the submitted molecule is CH3NH2 or CH3NH3+, they both get the "basic" prefix and the calculated p K a is 10.08.
Definition of the acidic prefix
De-protonated negative ions are considered as de-protonated acidic sites , therefore "acidic" prefix is used for them. The neutral acidic sites are predefined in the p K a calculator and they also have "acidic" prefix, e.g. if submitted molecule is CH3COOH or CH3COO- , they both get the "acidic" prefix and p K a is 4.54.
Multiprotic molecules
When a molecule has more than one ionisable atom, it is called a multiprotic compound. For these types of molecules we need to distinguish between micro and macro acidic dissociation constants. The micro acidic dissociation constant is obtained from the equilibrium concentration of the conjugated acid-base pairs. The macro acidic dissociation constant is obtained from the global mass and charge conservation law. When a molecule has N ionisable sites, the total number of microspecies in the solution is 2N.
Example
To better understand the difference between micro and macro constants we consider ionization equilibrium of a triprotic acid AH3. Referring to the different deprotonation sites of the AH3 molecule we introduce the upper indexes of the protons:
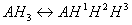
The ionization process of the AH1H2H3 molecule in aqueous solution is described with 12 equilibrium reactions. Microspecies and their charge are summarized in Table 1.
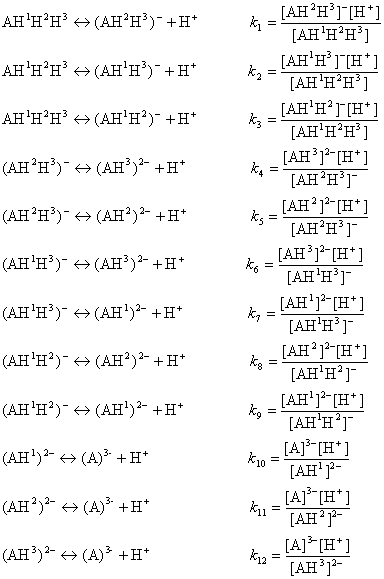
| Microspecies | charge |
|---|---|
| AH1H2H3 | 0 |
| AH1H2 , AH1H3 , AH2H3 | -1 |
| AH1 , AH2 , AH3 | -2 |
| A | -3 |
Tab. 1 Microspecies of AH3 and their charge
The AH3 molecule has three macro acidic constants since it is a triprotic acid. Macro acidic constants K1, K2, and K3 are obtained from the concentration of the microspecies:
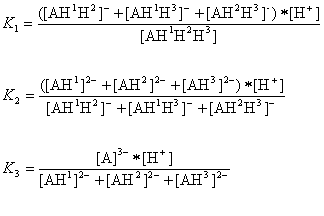
And the three macro p K a values of the AH3 molecule that would be obtained with routine laboratory measurements are as follows:
p K a,1=-log10( K 1)
p K a,2=-log10( K 2)
Examples
The following examples show the different acidic/basic dissociation processes and their related calculations.
Example #1
The ionisation steps of p -amino benzoic acid are outlined below. Calculated micro ionisation constants k1, k2, k3 and k4 are indicated on the arrows.
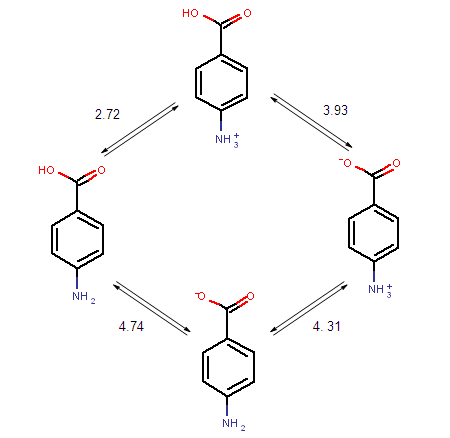 Fig. 1 Ionization steps of p -amino benzoic acid
Fig. 1 Ionization steps of p -amino benzoic acid
Below are the calculated and the experimental p K a values of p -amino benzoic acid:
Example #2
Imides and amides can have either acidic or basic character. The extent of amide/imide ionization at a given pH is determined by two acid dissociation constants: p K a,1 is assigned to the de-protonation step RNH 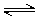 RN- + H+ and p K a,2 is assigned to the protonation step RNH2+
RN- + H+ and p K a,2 is assigned to the protonation step RNH2+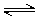 RNH + H+ .
RNH + H+ .
The ratio of anionic and cationic species depends on p K a,1, p K a,2 and the actual pH:
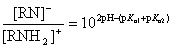
If 2pH - (p K a,1 + p K* a,2) > 0, de-protonation of the amide/imide is favoured, and the molecule is said to have an acidic character.
If 2pH - (p K a,1 + p K* a,2) < 0, protonation of amide/imide is favoured, and it is considered to have a basic character.
Chemists often want to know the ionization state of organic compounds at pH 7.4 (the pH value of human blood). In general, the macro p K as of amide/imide compounds are calculated and their acidic or basic character determined by the above formulas at pH 7.4. We give as an example two amides: phthalamide and 2-pyridone.
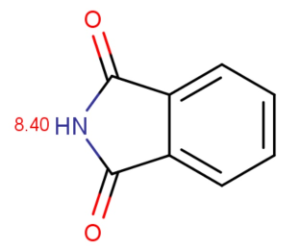
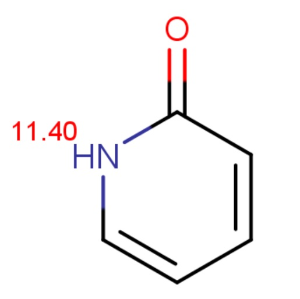
Calculated and measured p K a values of phthalimide and 2-pyridone are given in Table 2.
| Compound | Calculated p K a | Observed p K a |
|---|---|---|
| phtalimide | 8.40 | 8.30 |
| 2-pyridone | 11.40 | 11.70 |
Tab. 2 Calculated and measured pKa values of phthalimide and 2-pyridone
Example #3
The value of ionization constants of conjugated acid/base pairs usually falls between 10-2 and 1016 , so these limits are generally used to predict the p K a. When an ionisable site in the molecule has an ever weaker basic or acidic character, the ionisable site can be involved in the calculation by increasing the calculation range.
The molecule depicted below contains a very weak acidic N atom. First, macro p K a is calculated with default limits predefined between 10-2 and 1016 . Then macro p K a is calculated with altered limits defined between 10-50 and 1050 .
{info} Changing the default settings of macro p K a calculation can be done in the Tools > Options > pKa menu of MarvinSketch.
Calculated and observed acidity constants are summarised in Table 3. Measured p K as are taken from Clark et al.
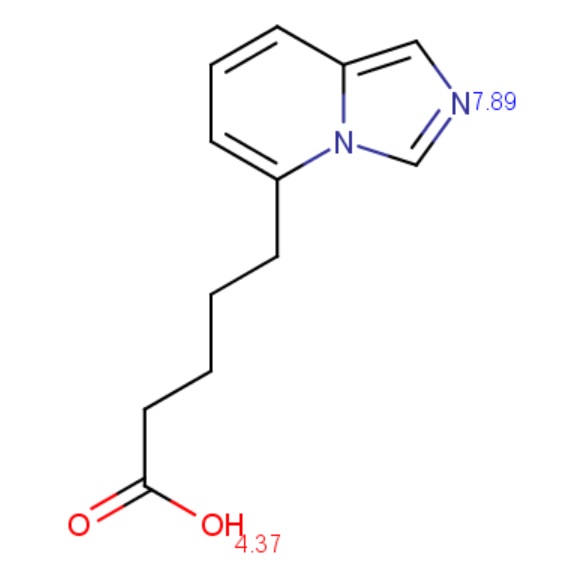
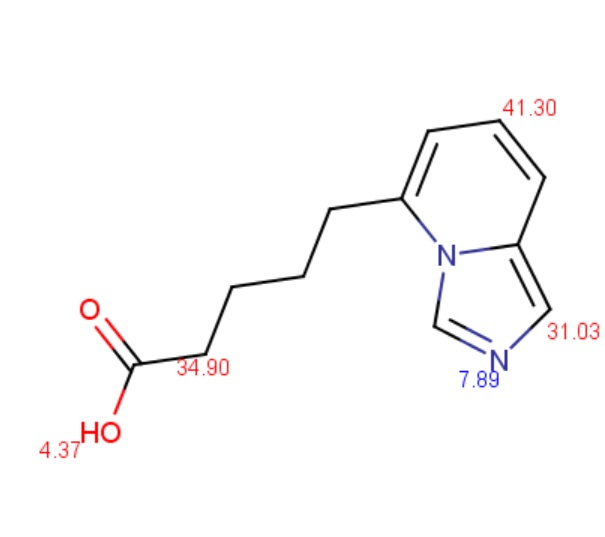
| p K a | First calc. | Second calc. | Observed |
|---|---|---|---|
| p K a,1 | 4.37 | 4.37 | 4.51 |
| p Kb ,1 | 7.89 | 7.89 | 6.01 |
| p K a,2 | - | 31.03 | - |
Table 3. The first three calculated and measured acidity constants
References
-
Prediction of dissociation constant using microconstants, J. Szegezdi and F. Csizmadia, 27th ACS National Meeting, Anaheim, California, March 28-April 1, 2004
-
A method for calculating the pKa values of small and large molecules, J. Szegezdi and F. Csizmadia, American Chemical Society Spring meeting, March 25-29th, 2007
-
Clark, F. H.; Cahoon, N. M., J. Pharm. Sci. , 1987 , 76 , 8, 611-620
-
Dixon, S. L.; Jurs, P. C., J. Comp. Chem. , 1993 , 14 , 12, 1460-1467; doi
-
Csizmadia, F.; Tsantili-Kakoulidou, A.; Panderi, I.; Darvas, F., J. Pharm. Sci. , 1997 , 86 , 7, 865-871; doi
